清一色において六門張/五門張等は何種あるか。あるいは普通の手の一向聴には、どのようなパターンがあるか。その一向聴段階では何を切ったら聴牌チャンスがもっとも大きくなるか。このような麻雀の数理的側面は、中国ではほとんど研究されなかった。しかし大正末期、麻雀が伝来すると同時に、日本では盛んに研究された。
今回のテーマはその中の聴牌効率、すなわち「一向聴段階で何を切ったら聴牌チャンスがもっとも大きくなるか」というものである。K式のKとは草創期の重鎮である川崎備寛氏のこと、すなわちK式とは川崎式算術法という意味である。
といっても別に難しい数式が出てくるわけではない。手牌八張の整理戦術として、単純に聴牌への有効牌の多寡から打牌を選択するのがよろしいと論じたものである(「麻雀の打ち方(大泉書店172p〜)」)。それを改めてK式算出法などと称しては、川崎氏は却って不本意に思うかも知れない。。。。
といってもこれはσ(-_-)が命名したわけではない。A式確率法(天野式)、N式数学法(沼崎式)と比較するために、仮に天野大三氏がつけた名称である。そして今後、A式確率法もN式数学法も紹介して行く予定なので、その面からの分かりやすさを考え本カテゴリーでもK式算出法と呼称することにする。
(A)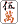 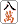 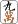 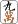 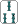 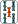  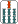
ここで何を切ったら聴牌への有効牌がもっとも多いか。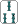 や や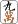 は考えるまでもない。そこで は考えるまでもない。そこで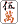 か か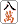 ということになる。しかし ということになる。しかし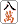 切りでは万子6種21枚、 切りでは万子6種21枚、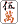 切りでは万子4種13枚である(筒子に関しては両者同数)。そこでK式算出法では 切りでは万子4種13枚である(筒子に関しては両者同数)。そこでK式算出法では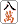 切りがもっとも有効と考える。 切りがもっとも有効と考える。
(B)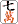 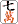 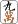 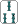 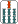   
打牌候補としては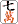 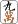 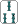 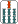 であるが、これも であるが、これも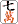 切りなど考える余地はない。で、 切りなど考える余地はない。で、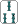 切りは8種25枚、 切りは8種25枚、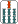 切りは8種28枚、 切りは8種28枚、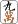 切りは10種33枚なので、 切りは10種33枚なので、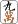 切りがもっとも有効と考える。 切りがもっとも有効と考える。
(C)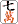 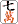 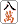  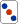 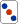  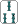
これも単純に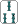 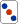 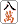 をそれぞれチェックすると、 をそれぞれチェックすると、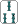 切りでは9種29枚、 切りでは9種29枚、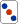 切りでは9種32枚、 切りでは9種32枚、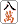 切りでは11種32枚、そこで 切りでは11種32枚、そこで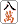 切りがもっとも有効と考える。 切りがもっとも有効と考える。
以上のように考えるのがK式算出法というか、手牌八張の整理戦術。何の問題も感じられないが、ここにはチーとかポンの可能性に対する視点がない。そこでチーポンの可能性にも目を向け、それを数値化して聴牌効率の優劣を論じたのが、次に紹介するA式確率法である。
|
や
は考えるまでもない。そこで
か
ということになる。しかし
切りでは万子6種21枚、
切りでは万子4種13枚である(筒子に関しては両者同数)。そこでK式算出法では
切りがもっとも有効と考える。
であるが、これも
切りなど考える余地はない。で、
切りは8種25枚、
切りは8種28枚、
切りは10種33枚なので、
切りがもっとも有効と考える。
をそれぞれチェックすると、
切りでは9種29枚、
切りでは9種32枚、
切りでは11種32枚、そこで
切りがもっとも有効と考える。